二叉树的四种遍历

对于一个给定的二叉树，有四种遍历方式：先序遍历、中序遍历、后序遍历、层次遍历。

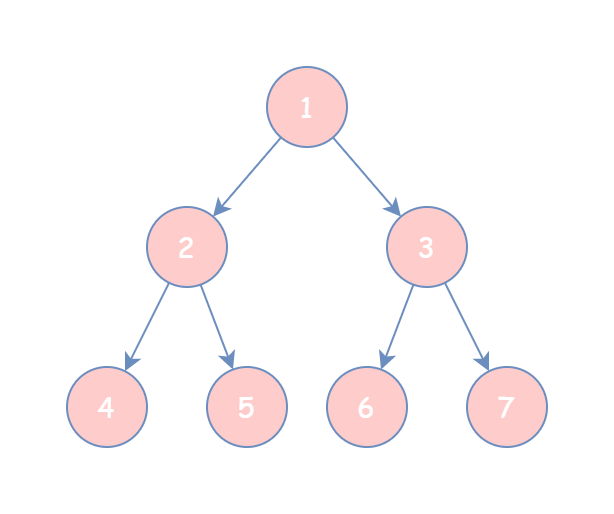
• 前序遍历：根节点 -> 左孩子 -> 右孩子，遍历结果为 1 2 4 5 3 6 7；
• 中序遍历：左孩子 -> 根节点 -> 右孩子，遍历结果为 4 2 5 1 6 3 7；
• 后序遍历：左孩子 -> 右孩子 -> 根节点，遍历结果为 4 5 2 6 7 3 1；
• 层序遍历：按照每一层从左向右的方式进行遍历，遍历结果为 1 2 3 4 5 6 7。

1 前序遍历

144. 二叉树的前序遍历

复杂度分析

• 时间复杂度：O(n)，n 为节点数，访问每个节点恰好一次。

• 空间复杂度：O(h)，h 为树的高度。最坏情况下需要空间 O(n)，平均情况为 O(logn)。

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        def pre_order(root):
            if root:
                res.append(root.val)
                pre_order(root.left)
                pre_order(root.right)
        res = []
        pre_order(root)
        return res

2 中序遍历

94. 二叉树的中序遍历

复杂度分析

• 时间复杂度：O(n)，n 为节点数，访问每个节点恰好一次。

• 空间复杂度：O(h)，h 为树的高度。最坏情况下需要空间 O(n)，平均情况为 O(logn)。

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        def in_order(root):
            if root:
                in_order(root.left)
                res.append(root.val)
                in_order(root.right)
        res = []
        in_order(root)
        return res

3 后序遍历

145. 二叉树的后序遍历

复杂度分析

• 时间复杂度：O(n)，n 为节点数，访问每个节点恰好一次。

• 空间复杂度：O(h)，h 为树的高度。最坏情况下需要空间 O(n)，平均情况为 O(logn)。

class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        def post_order(root):
            if root:
                post_order(root.left)
                post_order(root.right)
                res.append(root.val)
        res = []
        post_order(root)
        return res

4 层序遍历

102. 二叉树的层序遍历

复杂度分析

• 时间复杂度：O(n)，n 为节点数，访问每个节点恰好一次。

• 空间复杂度：O(h)，h 为树的高度。最坏情况下需要空间 O(n)，平均情况为 O(logn)。

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        res = []
        queue = collections.deque()
        queue.append(root)
        while queue:
            level = []
            for _ in range(len(queue)):
                node = queue.popleft()
                level.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            res.append(level)
        return res